A good way to start off with the proof of the area of a triangle is to use the area of a rectangle to quickly derive the area of a right triangle.
Start with a rectangle ABCD and let h be the height and b be the base as shown below:
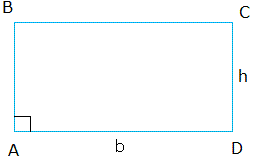
The area of this rectangle is b × h
However, if we draw a diagonal from one vertex, it will break the rectangle into two congruent or equal triangles.
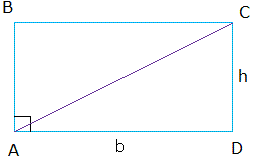
The area of each triangle is half the area of the rectangle. For example, the area of triangle ABC is 1/2(b × h). Does that make sense?